|
2A: Maxwell's Equations
and Electrostatics
Feynman
Simplified
2A covers
the first
quarter of
Volume 2, the freshman course, of The Feynman Lectures
on Physics. The topics we explore include:
- Maxwell’s Equations of Electromagnetism
- Algebra & Calculus of Vector
Fields
- Gauss’ & Stokes’ Theorems
- Electrostatics with Conductors
& Dielectrics
- Electrostatic Energy
- Electricity in the Atmosphere
- Why
The Same Equations Appear Throughout Physics
Excerpt:
Vector
Fields
Another
example of a vector field is heat flow. The figure below depicts heat
flowing
from a hot spot (white circle) above an isothermal plane (gray area at
bottom). The boxed region of the main image is enlarged at the right.
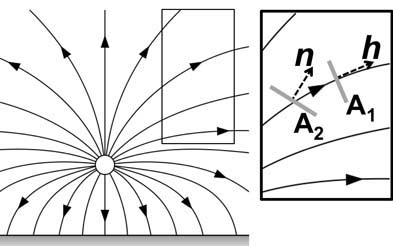
The
vector h
indicates heat passing a selected point. Two planes (shown as
gray bars) have areas A1 and A2. As the figure
indicates, A1
is
perpendicular to h
but A2 is not. We wish to know the amount of heat
flowing through each plane. The vector n is a unit vector normal to
plane A22.
Unit vectors have length 1.
We will define h
in terms of the amount of thermal energy passing a
selected point per unit time per unit area. We first define a surface
that is perpendicular to h that has an
infinitesimal area ΔA. We also
define ΔJ to be the amount of thermal energy passing through ΔA per
unit time. The equation for h is:
h
= (ΔJ/ΔA) eh
Here eh is a unit vector
in the h direction.
|



