|
 Xmas Special - 40% off selected print books. See below Xmas Special - 40% off selected print books. See below
In Part 1 of this newsletter, we explored Zeno’s paradox and the EPR paradox.
In Zeno’s paradox, the swift Achilles races the plodding Yertle, who has a head start. Zeno correctly said there is an infinitely repeating cycle of {Achilles runs to where Yertle was, while Yertle crawls forward and stays ahead}. But Zeno was wrong to believe that infinitely many cycles require an infinite amount of time. Infinite series can have finite sums.
To be specific, assume Achilles runs 10x faster than Yertle, who begins with a 100-meter head start. In cycle 1, Achilles runs 100m while Yertle crawls 10m. In cycle 2, Achilles runs 10m while Yertle crawls 1m, … ad infinitum. In meters, Achilles’ total distance A in this infinite series of cycles is:
A = 100 + 10 + 1 + 0.1 + 0.01 +…. = 111.11… = 1000/9
Meanwhile, Yertle’s total distance Y is:
Y = 10 + 1 + 0.1 + 0.01 + 0.001 +… = 11.111… = 100/9
A = 10 Y, matching Achilles’ 10x faster speed.
A – Y = 900/9 = 100m, is Yertle’s head start.
Clearly, both run their distances in equal and finite times, after which Achilles takes the lead.
The EPR paradox of quantum mechanics (QM) addresses the meaning of reality and the validity of locality, special relativity’s dictum that no thing or influence can move through space faster than c, the speed of light. Locality precludes separated particles from interacting instantaneously. We explored Carlo Rovelli’s solution to the locality paradox in Part 1. Here, let’s explore the meaning of reality: are particle properties real before being observed.
Let’s recall our EPR experiment: each second, a source produces two photons that fly off in exactly opposite directions, with exactly opposite spins. Spin is a particle’s intrinsic angular momentum, and QM says the only vertical spin values photons can have are UP and DOWN. Alice is 15m to the left of the source, and Bob is 15m to its right. Both physicists measure the vertical spins of photons that come their way.
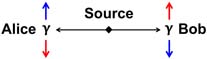
QM says each photon pair exists in one entangled quantum state. When their spins are measured, each photon is 50% likely to be UP and 50% likely to be DOWN, but entanglement ensures the two photons always have opposite spins, to conserve angular momentum (either the blue or red combinations above).
This experiment has actually been performed several times, with separations as large as 147 km. The results are always Alice and Bob each measure 50% UP and 50% DOWN, with Alice and Bob always measuring opposite spins.
QM proponents claim this proves some properties of particles, like spin, are not real — they have no definite values — until those properties are measured. Niels Bohr said: “nothing exists until it is measured.”
But proponents of classical physics, which assumes locality and the reality of all measurable quantities, have a quite different interpretation of this EPR experiment.
Classicists said the two photons have definite spins from the instant they are produced until the instant their spins are measured. Carlo Rovelli makes an interesting analogy: a factory produces pairs of gloves, with each pair having one right hand and one left hand glove. At the end of the assembly line, a worker sends a randomly selected glove to Alice, and sends its partner to Bob. Each physicist gets a right hand glove 50% of the time, and they always get opposite-handed gloves. No magic here — locality and reality are both upheld.
QM and classical physics can both explain the experiment’s outcomes. So, the compelling question is: how can we know if the photon spins have real definite values before we measure them. Physicists took decades to solve this dilemma.
The Irish theorist J. S. Bell suggested rotating Bob’s spin detector by angle θ, as shown below. Here, we are looking along the axis of the photons’ motion. One photon is coming out of the screen toward Alice, while the other photon is going into the screen toward Bob. I displaced the two circles for clarity; they actually are on top of one another in this view. Alice measures spins vertically, while Bob measures spins along a tilted axis. The solid arrows below indicate the measurement axes.
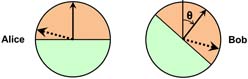
Classically, the two photons always have definite spins; they are produced with spins in a random orientation that remains fixed. Alice’s photon’s spin can point at any angle around the circle, while Bob’s photon always points opposite to Alice’s. The dotted arrows above show one possible orientation. Alice measures any spin orientation in her orange zone as UP, and any spin in her green zone as DOWN. Similarly for Bob, but his orange and green zones are rotated by angle θ.
Assign spin UP the numerical value +1, and spin DOWN the value –1. We then define correlation C to be the average over all possible spin orientations of the product of Alice’s and Bob’s spin values. By symmetry, we need only consider the range 0 ≤ θ ≤ π radians. The correlation C-CL for any classical theory, where spins are definite before measurement, is:
C-CL = –1 + 2 θ/π
We can check this equation for some simple θ’s. For θ=0, we have the original setup in which Bob’s spin is always opposite Alice’s, so C=–1. For θ=π, Bob’s new UP is what his DOWN was before, and vice versa; with his inverted values, Bob always measures the same spin as Alice, so C=+1. For θ=π/2, Bob and Alice agree half the time and disagree half the time, so C=0.
In QM, we employ rotation operators (see my books) and obtain:
C-QM = – cosθ
You can check that C-QM equals C-CL at θ=0, π, and π/2. But, C-QM (blue curve below) and C-CL (red line) differ at other angles, as shown below.
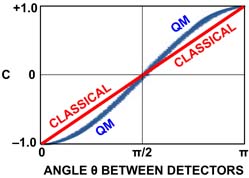
Called Bell’s Inequality, this test distinguishes QM from all classical theories in which spins have definite values before being observed, including all hidden variable theories.
Three famous experiments conclusively proved nature is precisely described by QM and not by any classical theory, with or without hidden variables.
Thus, particle properties, such as spin, do not have definite values while undisturbed; their values become definite when they interact incoherently with something else, as typically happens in our measurements.
Locality and the universal speed limit c are still valid principles if we accept Rovelli’s Relational QM.
For more about quantum mechanics and the EPR paradox see my books Feynman Simplified Part 3 (paperback), Feynman Simplified 3C (ebook), or Quantum Mechanics 1 – 5 (short ebooks).
|