|
I am greatly relieved to announce that Feynman Simplified has
finally been delivered after 22 months of hard labor. I thank my
tireless and ruthless editor, my beautiful bride (of 46 years), Joan
Piccioni.
Feynman Simplified
brings Feynman’s genius and comprehensive understanding of nature to a
broader audience: those who don’t walk on water. This is Real Science for Real People. You can view the selection on our website. So far, over 5,000 Feynman Simplified eBooks have been purchased.
As 2015 draws to a close, we also celebrate the one hundredth anniversary of Einstein’s greatest achievement: the General Theory of Relativity.

General
relativity is the most profound theory of physics, and is regarded by
many as the greatest achievement of a single human mind. It precisely
describes the motion of any object, with any velocity, and with any
acceleration. General relativity is a comprehensive theory of gravity,
energy, space and time. It enables us to understand the universe, and
its most exotic denizens: neutrons stars, black holes, and quasars.
Ten
years earlier, Einstein published his special theory of relativity.
This theory is “special” in that it applies only to an especially simple
situation: motion at a constant velocity. Special relativity
properly describes an enormous range of natural phenomena, and is the
most extensively and precisely tested principle in science. But it
cannot describe objects accelerated by forces, such as gravity.

Special
relativity supersedes Newton’s laws of motion, whereas general
relativity supersedes Newton’s theory of gravity — both gold standards
of science for over two hundred years.
Einstein excelled in describing profound truths with simple equations, the most famous being E=mc2. For general relativity, the field equation is:
G = 8π T
Here,
G represents the geometry of the universe, the curvature of spacetime,
and T represents everything in the universe, matter and energy. This
equation says:
Matter and energy tell spacetime how to curve;
spacetime tells matter and energy how to move.
Newton
said space and time are absolute, autonomous, and eternally immutable.
Einstein said space and time are dynamic, eternally changing, and
definable only in relation to something else.
For
Newton, space and time are like a Shakespearean stage upon which the
actors, mass and energy, play their parts. For Einstein, spacetime is
like a Cirque du Soleil stage that plays an active role in the drama of
the cosmos.
With precise space-telescope measurements, general relativity yields this simple equation for the evolution of our universe:
3 H2 = 8π ε
Here,
H is the Hubble expansion rate, and ε is the density of all forms of
energy, including light, normal matter, dark matter, and dark energy.
With measured values of H and ε, we can calculate how the universe has
grown in the past, and what its future will be.
Since
the universe is now expanding, we know that H is now greater than
zero. And since ε is never zero, H can never be zero — H can never
pass through zero and change from positive to negative.
Looking to the future, this means our universe will always expand, and will never collapse into a Big Crunch.
Now
let’s look back into the past to see where we came from. Imagine that
we had a movie of our universe from long ago to today, and that we can
play that movie backwards, so that the cosmic clock spins in reverse. We
would see a universe that is always contracting — always, that is,
until its size becomes zero.
This
means our universe must have had a beginning, a Big Bang, an instant
when everything and everywhere was contained within a tiny ball of
almost zero size. From the latest satellite data, we know that instant
was 13.82 billion years ago, with an uncertainty of ±0.05 billion years.
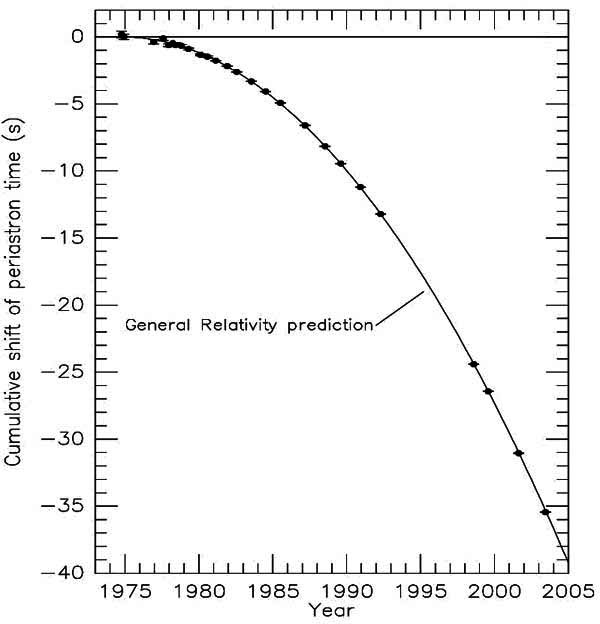
One
last juicy morsel: general relativity says two massive stars orbiting
one another must emit energy in the form of gravity waves, ripples in
the fabric of spacetime. That continuous energy loss causes the stars to
orbit ever closer, and eventually merge.
Sixty
years after Einstein published general relativity, Russell Hulse and
Joseph Taylor observed two neutron stars orbiting one another once every
8 hours. Over the next 30 years, astronomers have observed this 8-hour
orbital period slowly decreasing as the neutron stars move closer
together. The measured rate of change of the orbital period is 76.5±0.8
seconds per million years.
For these neutron stars, general relativity predicts an orbital period change of 75.8 seconds per million years.
This
graph illustrates the excellent agreement between measurements (black
dots with uncertainty bars), and general relativity (parabolic curve).
Seventeen
years before the discovery of the neutron, and 52 years before the
first observation of a neutron star, Einstein sat at his desk, with only
paper and pen, and conceived the theory that precisely predicts a
completely unexpected phenomenon occurring 120,000 trillion miles from
Earth.
This is a stunning demonstration of the power of the human mind.

Best Regards,
Robert
Dec 15, 2015
Note: Previous newsletters can be found on my website.
|