|
1B: Harmonic Oscillators
& Thermodynamics
Feynman Simplified 1B covers the 2nd
quarter of the freshman course of The Feynman Lectures on Physics.
The topics we explore include:
- Harmonic Oscillators, Resonances, and
Transients
- Kinetic Theory of Gases
- Statistical Mechanics
- Thermodynamics
Excerpt:
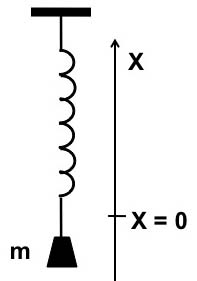
The
simplest mechanical example of behavior governed by a linear
differential equation is a mass on a spring, illustrated in Figure
12-1. Here m is the mass, x is the vertical height, and x = 0 is the
equilibrium height, the height at which that mass can rest motionless
on this spring.
We’ll
assume the spring is ideal, perfectly elastic and obeys Hooke’s law: it
exerts a force F = –kx, where k is the spring constant. The minus sign
signifies that the force opposes the displacement x: if we compress the
spring by moving the mass to +x, the spring’s force is directed
downward, and vice versa. The differential equation is then:
F = ma = –kx
d2x/dt2 = –(k/m) x
Excerpt:
The
figure below shows a collision between two different atoms as viewed in
their center of mass (CM). The diagonal line is the axis of symmetry,
which passes through the centers of both atoms and their point of
contact. The symmetry axis is rotated from the incoming direction by
the angle ø.
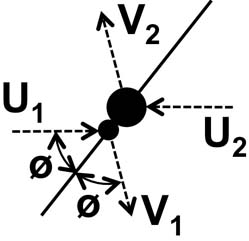
Call
the
masses of the two atoms m1 and m2. The atoms’ velocities are u1 and u2
before the collision and v1 and v2 afterward.
We will shortly show that the magnitude of each atom’s
velocity, its
speed, is the same before and after the collision. With that we see the
v’s are at the same angles to the axis of symmetry as are the u’s. Thus
the scattering angle of each atom is: θ=π–2ø.
|






